Magnetism

An electron possesses a “spin” that gives it a magnetic moment, causing it to behave like a tiny magnet. If a substance is diamagnetic, it will weigh less in a magnetic field, and weigh more if paramagnetic. Diamagnetism is a much weaker effect than paramagnetism.

Diamagnetic:

All the electrons are spin-paired, weakly repelled by magnetic field, low spin, goes to stronger field (anisotropic), big splitting, and need Lewis dot diagrams.

Paramagnetic:

Has 1 or more unpaired electrons, weakly attracted by magnetic field, high-spin, goes to weaker field (isotropic), small splitting, and do not need Lewis dot diagrams.

Examples of diamagnetic compounds are N₂ and F₂, and C-C, examples of paramagnetic compounds are O₂, NO, and B-B. Examples of neither, are glass, plastics, rubber, and wood.

Diamagnetism is also associated with superconductors (above the Tc). In a paramagnetic solid, the electrons on 1 atom or ion do not influence the unpaired electrons on neighboring atoms or ions.

An electron can jump half an angstrom from a metal, so metals a few angstroms away cannot feel each other.

Ferromagnetism, antiferromagnetism, and ferrimagnetism.

The classical magnet is ferromagnetism, known as a permanent magnet, and is much stronger than paramagnetism, by as much as up to 1 million times stronger. Ferromagnetism arises when the unpaired eletrons of the atoms or ions in a solid are influenced by the orientations of the electrons in neighboring atoms or ions. The most stable (lowest energy) arrangement is when the spins of electrons on adjacent atoms or ions are aligned in the same direction.

The only transition metals that are ferromagnetic are Fe, Co, and Ni (all collinear). Some particularly powerful ferromagnets are found in compounds containing both transition metals and lanthanide metals, such as SmCo₅ and Nd₂Fe₁₄B (both collinear). Some noncollinear ferromagnets include chiral magnets, such as MnSi, FeGe, and Cu₂OSeO₃.

When half of the atoms have their unpaired electrons in the opposite spin direction on neighboring atom, are antiferromagnetism. But when there aren't half as many ferromagnetic and antiferromagnetic atoms, are ferrimagnetic (i.e., 2/3rd point north and 1/3rd point south, compared to 50/50). This can happen because the magnetic centers have different numbers of unpaired electrons (such as NiMnO₃, which is noncollinear), because the number of magnetic sites aligned in 1 direction is larger than the number aligned in the other direction (such as Y₃Fe₅O₁₂, which is noncollinear), or both (such as Fe₃O₄, which is collinear spin arrangement).

Examples of antiferromagnetic substances are Cr metal, FeMn alloys, and some transition-metal oxides such as Fe₂O₃ (noncollinear), LaFeO₃ (generally collinear), CuO (noncollinear), MnO, and NiO (last 2 collinear).

Ferromagnets and ferrimagnets are strongly attracted to a magnetic field, while antiferromagnets usually have no attraction.

In classical physics, a material cannot be both ferromagnetic and diamagnetic at the same time (every superconductor is a perfect diamagnet, but ordinary diamagnetic material are not necessarily superconductors). In quantum mechanics, a material can exhibit both ferromagnetic and paramagnetic behavior simultaneously, but these behaviors would occur in different parts of the material. Ferromagnetic materials have magnetic moments that align with an external magnetic field, but much stronger than in paramagnetic materials, but unlike paramagnetic materials, the alignment in ferromagnets do not disppear when the external field is removed. Ferromagnets also cannot be spin-paired in classical physics.

In quantum mechanics, there are some cases where seemingly fully spin-paired materials can exhibit ferromagnetic behavior. One example is the phenomenon of Hund's rules violation. In certain materials and specific conditions, deviations from Hund's rules can occur, leading to a non-0 magnetic moment even in the presence of spin-paired electrons.

An example of a superconductors perfect diamagnetism, is magnetic levitation. This occurs when a magnet is placed over a superconductor cooled below its critical temperature, causing it to levitate due to strong diamagnetic currents generated by the superconductor that oppose the magnet's field.

Ferromagnets, ferrimagnets, and antiferromagnets all become paramagnetic when heated above a critical temperature. For the 1st 2, are called Curie temperature (T_C, and the last 1, called Néel temperature (T_N). This happens when the thermal energy is sufficient to overcome the forces determining the spin directions of the electrons.

Ferromagnets break rotational symmetry, ferrimagnets (Fe₃O₄) partially break rotational symmetry, antiferromagnets break translational symmetry, paramagnets (Al, Pt) and diamagnets (Cu, Bi) have no broken symmetry.

The concept of low-resistance parallel, applies to ferromagnets, and high-resistance anti-parallel, applies to antiferromagnets, as magnetoresistance effects. They don't apply to diamagnets since they don't have spin alignment or net magnetization, and only weakly affects paramagnets.

Case-study.

Ferromagnetism with the surprisingly high Curie temperature (T_C) of 600 K has been reported in La-doped CaB₆ and in HfO_2-x films where the T_C is 500 K. The origin of the spontaneous moments in these closed-shell materials is, as of 2005, are still unexplained.

In rare circumstances, the ferromagnetism can be observed in compounds consisting of only s-block and p-block elements, such as rubidium sesquioxide. In contrast to the many magnetic compounds containing transition metal or lanthanide atoms, ferromagnetism based on atoms from the 2p series is very rare. Density functional calculations show the existing compound rubidium sesquioxide is a ferromagnet with an estimated Curie temperature of 300 K, unprecedented in p-electron magnetism. The magnetic moment is carried by the anion. Rubidium sesquioxide is a conductor, but only for the minority spin electrons (a so-called “half-metal”). Rb₄O₆ is an intrinsic ferromagnet in which the magnetic moment is carried exclusively by the p-electrons of the oxygen anions.

Free radicals.

If an atom/molecule contains 1 or more unpaired electrons and is capable of independent existence, it is referred to as a “free radical.” Atoms possess electrons that are usually associated in pairs. Each pair moves in a defined space around the nucleus referred to as the atomic/molecular orbital. 1 electron of the pair has spin quantum number +1/2 and the other -1/2. When the electrons are in opposite spins, the electronic state is singlet and referred to as “ground state.” Electrons with the same spin are “triplet state,” but if singlet molecules absorb energy without changing spin, the molecule is in an “excited singlet state.” Free radicals can be generated as products of homolytic, heterolytic, or redox reactions, producing either charged or uncharged radical species.

History.

Diamagnetism was discovered by Anton Brugmans in 1778 when he realized magnetic fields repelled bismuth, but the name was given by Michael Faraday in Sept. 1845 as dimagnetic, then suggested to change to diamagnetic in a Dec. 10, 1845 letter from William Whewell to Faraday. Faraday designated the term paramagnetic in 1851.

Quantum spin liquids.

A quantum spin liquid is a system with magnetic moments where there are no broken symmetries. The 1st quantum spin liquid to be discovered was in herbertsmithite (ZnCu₃(OH)₆Cl₂) in 2012. There, it has a kagome lattice structure, where the Cu²⁺ ions form a network of corner-sharing triangles, so the spins are highly frustrated, preventing them from ordering even at low temperatures, leading to a spin liquid state. And although cesium chlorocuprate (Cs₂CuCl₄ was discovered before herbertsmithite (by 2001), herbertsmithite is considered to be the 1st true quantum spin liquid, as it shows no magnetic order even at extremely low temperatures. Both of them were discovered via neutron scattering experiments, revealing spinon excitations.

As of early 2025, there are no currently known quantum spin liquids in bulk materials.

Type	Broken symmetry?	Long-range order?	Spin correlation	Excitations
Ferromagnet	Rotational (fully broken)	Yes	Classical	Magnons
Antiferromagnet	Translational	Yes	Classical	Magnons
Ferrimagnet	Partially rotational (partially broken)	Yes	Classical	Magnons
Diamagnet	None	No	None	Orbital response
Paramagnet	None	No	Weak (thermal)	Uncorrelated spins
Quantum spin liquids	None	No	Strong (quantum entanglement)	Spinons, emergent gauge fields

History of quantum magnetism.

This starts in 1920, with the Ising, or Ising-Lenz model, which is a mathematical model of ferromanetism in statistical mechanics. This model consists of discrete variables that represent magnetic dipole moments of atomics spins that can only be in +1 or -1 state. If J_ij > 0, it is ferromagnetic (both i and j are spin-up). If J_ij < 0, it is antiferromagnetic, meaning i is spin-up and j is spin-down.

Then came the quantum Heisenberg model, in the late 1920s.

In 1931, came the general form of eigenfunctions (Bethe's Ansatz).

In 1938, came the ground state energy by Hulthen.

In 1962, came the S = 1 excitation spectrum, by des Cloiseaux and Pearson).

In 1981, came the S = 1/2 excitation spectrum by Faddeev and Takhtajan.

Up through the 1980s, work on magnetism focused either on ordered phases of classical and quantum models (and their defects), or on special features of quantum models in 1-space dimension (solvable by Bethe's Ansatz).

1. What does it mean when they say in condensed matter physics, if you break time-reversal symmetry, you have magnetism?

Time-reversal symmetry means that the equations describing a system are unchanged if you flip the direction of time: t -> -t.

For particles, this operation reverses certain quantities:

Momentum: p -> -p
Angular momentum / spin: S -> -S
Magnetic field: B -> -B

So, under time-reversal symmetry, any magnetic dipole or current loop flips direction. So with a spin-up electron, applying time-reversal symmetry gives you spin-down. Magnetism arises from spins and orbital currents, which are odd under time reversal.

If a material has no net magnetization, spin-up and spin-down are equally populated -> the system can still respect time-reversal symmetry. But if the system spontaneously chooses one orientation (say, most spins up -> ferromagnetism), time-reversal symmetry is broken because the state is not invariant under reversal (spin-up -> spin-down).

So the statement “if you break time-reversal symmetry, you have magnetism” means the only common way condensed matter systems spontaneously break time-reversal symmetry is through magnetic order (ferromagnetism, antiferromagnetism, etc.).

Strictly speaking: breaking ime-reversal symmetry implies magnetism (some kind of ordering involving spins or currents), but not all magnetism must break time-reversal symmetry locally. For example:

-Ferromagnets break time-reversal symmetry (obvious).
-Antiferromagnets also break time-reversal symmetry, even though net magnetization is 0, because the microscopic spin arrangement isn’t invariant under time-reversal.

There are exotic cases too: superconductors with certain pairing states (like chiral p-wave) can break time-reversal symmetry without conventional magnetism, but even there, tiny spontaneous currents or internal fields appear.

So while time-reversal symmetry says “flip all spins and currents,” if the system is unchanged, time-reversal symmetry is preserved (no magnetism). If not, you’ve got magnetism (or something that produces effective internal magnetic fields).

Microwave-assisted switching.

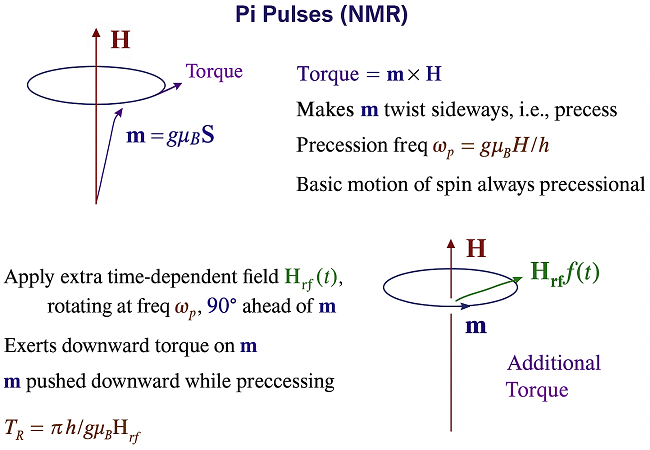
Precession is the circular (or spiral) motion of the magnetic moment around the field direction, which is the basic dynamic motion of spins in a magnetic field.

Precession refers to the way the magnetization vector of a magnetic particle moves in response to an applied magnetic field. A magnetic particle (or spin system) has a net magnetic moment. When placed in a magnetic field B₀, that moment experiences a torque, which causes the precession. Instead of aligning instantly with the field, the moment rotates (or "precesses") around the direction of the field, much like how a spinning top wobbles around the vertical axis under gravity. This rotation happens at the Larmor frequency (frequency of precession), given by ω₀ = γB₀ where γ is the gyromagnetic ratio. Driving the system with a microwave field at this frequency can excite uniform precession (all spins roughly in phase). In ferromagnetic resonance (FMR), the entire magnetization vector of a ferromagnet precesses around the effective field (which includes applied field + internal demagnetizing fields).

A simple resonant pi-pulse that flips nuclear spins in NMR does not reliably reverse the magnetization of a ferromagnetic nanoparticle, because the magnet’s dynamics are nonlinear and the uniform precession (the “macrospin” mode) couples strongly to many spin-wave / magnetostatic modes. That coupling leads to parametric (Suhl) instabilities that steal energy from the uniform mode and break the coherent rotation you’re trying to force.

So when you try to flip the magnetization with a strong radiofrequency pulse (like the pi-pulse in NMR), instead of simply flipping, the magnetization enters a complicated nonlinear precession. At high amplitudes, instabilities (like the Suhl instability) appear, where energy gets transferred into other spin-wave modes rather than producing a clean reversal.

Using radio-frequency or microwave pulses to manipulate the magnetization in ferromagnets or nanomagnets) is generally called microwave-assisted magnetization switching.

-In NMR, you flip nuclear spins with pi-pulses at the Larmor frequency.
-In ferromagnets, the analog would be driving the collective magnetization into reversal with a resonant microwave magnetic field.

This is studied under ferromagnetic resonance (FMR) and related dynamics, where the microwave field couples to precession of the magnetization.

The Suhl instability is 1 of the main limiting factors: at high drive power, energy gets pumped into spin-wave modes instead of coherent switching.

A spin-wave is the classical wave description: a collective oscillation of spins in a lattice, where neighboring spins precess out of phase. (A magnon is the quantized particle-like excitation of a collective spin-wave.).

Suhl discovered (1955-58) that when you pump the uniform mode strongly with microwaves:

Instead of just flipping the magnetization smoothly, the energy couples into spin-waves at finite wavelengths, creating parametric amplification of those modes. In quantum language, that means the uniform magnon mode (k = 0) decays into pairs of magnons at k ≠ 0. In classical language, that means the large-angle precession of magnetization destabilizes, and energy leaks into non-uniform oscillations.

This is why you can’t just apply a pi-pulse: the system fractures into these unstable excitations instead of rotating coherently. Can we reverse the magnetization of a magnetic particle by a similar pulse? The answer is no. The obstacle is a parametrically amplified dynamic instability discovered by Suhl (1955-58). To try to beat the Suhl instability 1 would have to apply specially phased and chirped pulses, studied by numerical solution of the spin dynamics in magnetic nanocylinders. We would have to understand ferromagnetic resonance and magnetostatic modes.

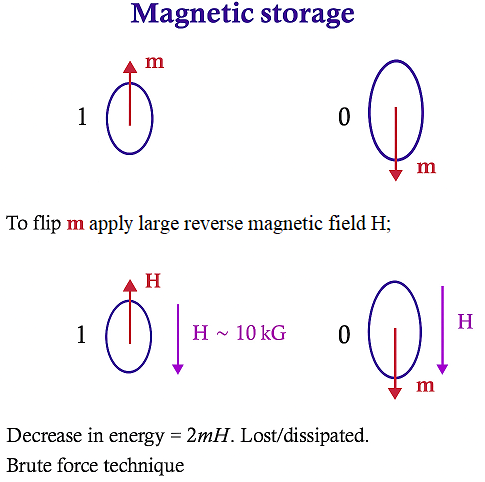
The magnets in the image aren’t big rod magnets, they are tiny magnetic domains or nanoparticles used for magnetic storage (like hard drives, MRAM, etc.). In a modern hard drive, each bit is stored in a magnetic grain that’s on the order of 10–20 nanometers across. In older hard drives, grains were larger, about 100 nm or more.

In magnetic RAM (MRAM) or spintronics research, people work with individual nanomagnets ~10–100 nm, often in thin-film form. So the “magnet” in the diagram really means a single-domain magnetic particle (or a little patch of magnetic film) whose net magnetization vector m points either up or down.

They’re tiny enough that quantum/statistical effects matter (thermal fluctuations can randomize them if they’re too small, called the superparamagnetic limit). And as this energy is not recovered, it’s dissipated as heat, is why it's called a “brute force technique.”